SciPy Distribution Example

This example shows how to use any of the SciPy distributions in Pystra. Here, we develop a simple model using the Generalized Extreme Value distribution.

Start off with the necessary imports:

import pystra as pr
from scipy.stats import genextreme as gev

Define the limit state function

def lsf(X1, X2, C):
    return X1 - X2 - C

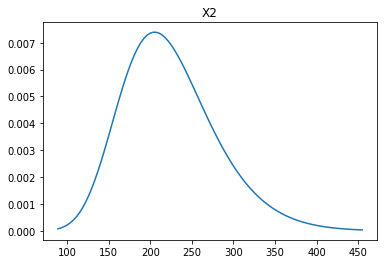
Create the GEV variable and plot that it is defined as intended:

X2 = pr.ScipyDist("X2", gev(c=0.1, loc=200, scale=50))
X2.plot()

Now create the limit state and stochastic model objects, and add the varaiables

limit_state = pr.LimitState(lsf)

model = pr.StochasticModel()
model.addVariable(pr.Normal("X1", 500, 100))
model.addVariable(X2)
model.addVariable(pr.Constant("C", 50))

Suppress the console output

options = pr.AnalysisOptions()
options.setPrintOutput(False)

Execute a FORM analysis

form = pr.Form(stochastic_model=model, limit_state=limit_state, analysis_options=options)
form.run()
form.showDetailedOutput()

======================================================
FORM
======================================================
Pf                       2.4939239502e-02
BetaHL                   1.9610046625
Model Evaluations        39
------------------------------------------------------
Variable            U_star             X_star        alpha
X1               -1.592128         340.787183    -0.811736
X2                1.144844         290.787242    +0.584025
C                      ---          50.000000          ---
======================================================

And then a SORM analysis (passing the existing FORM object for eficiency)

sorm = pr.Sorm(stochastic_model=model, limit_state=limit_state, form=form)
sorm.run()
sorm.showDetailedOutput()

======================================================

RESULTS FROM RUNNING SECOND ORDER RELIABILITY METHOD

Generalized reliability index:  1.9257163705247708
Probability of failure:         0.027069899329046212

Curavture 1: -0.07711553440911698
======================================================


======================================================
FORM/SORM
======================================================
Pf FORM                          2.4939239502e-02
Pf SORM Breitung                 2.7069899329e-02
Pf SORM Breitung HR      2.7546692546e-02
Beta_HL                          1.9610046625
Beta_G Breitung                  1.9257163705
Beta_G Breitung HR               1.9181390266
Model Evaluations                48
------------------------------------------------------
Curvature 1: -0.07711553440911698
------------------------------------------------------
Variable            U_star             X_star        alpha
X1               -1.592128         340.787183    -0.811736
X2                1.144844         290.787242    +0.584025
C                      ---          50.000000          ---
======================================================