Load Combinations

Pystra includes the class LoadCombination which can be used to analyse a structural reliability problem for different load cases. This example demonstrates the use of load combination cases with Pystra.

Example

This demonstration problem is adopted from Example 4 pp 190-1 from Sorensen, J.D. (2004), Notes in Structural Reliability Theory And Risk Analysis. The parameter values are slightly modified for demonstration.

Import Libraries

import pystra as ra
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

Define the limit state function

The LSF to be supplied in LoadCombination can be any valid Pystra LSF. Here we show how random variables and even constants (e.g. cg) can be passed through as Pystra objects, or can be hard-coded into the LSF.

def lsf(R, G, Q1, Q2, cg):
    return R - (cg*G + 0.8*Q1 + 0.2*Q2)

Define the Load and Resistance distributions

We define the distributions of the loads for the load combinations. Some loads will be time-invariant (e.g. permanent loads), while some will be combination random variables (e.g. winds, imposed loads). These combination loads require the definition of a point-in-time ('pit') distribution and a maximum ('max') distribtribution (typically annual maximum). Note that Pystra has built in distribution objects to convert between the two: MaxParent and Maximum.

For the combination loads, we define a dictionary which contains a key for each variable in the LSF, and a dictionary with the pit and max key values being the corresponding Pystra distribution objects.

Define the annual max distributions

Q1max = ra.Gumbel("Q1", 1, 0.2)  # Imposed Load
Q2max = ra.Gumbel("Q2", 1, 0.4)  # Wind Load

Next specifcy the parameters of inferred point-in-time parent distributions

Q1pit = ra.Gumbel("Q1", 0.89, 0.2)  # Imposed Load
Q2pit = ra.Gumbel("Q2", 0.77, 0.4)  # Wind Load
Q_dict = {'Q1': {'max': Q1max, 'pit': Q1pit},
          'Q2': {'max': Q2max, 'pit': Q2pit}}

And define any constants to be passed through

cg = ra.Constant("cg", 0.4)

Finally, define any other random variables in the problem

Rdist = ra.Lognormal("R", 2.0, 0.15)  # Resistance
Gdist = ra.Normal("G", 1, 0.1)  # Permanent Load (Other load variable)

Specify load combination cases

For this problem, in addition to the permanent loads, we’re interested in investigating the reliabilities for several load combinations: 1. Q1Q2_max: Where both Q1 and Q2 maximum distributions are considered simultaneously, as an obvious conservative estimation. 2. Q1_max: Q1 is maximum and Q2 is the point-in-time distribution. 3. Q2_max: Q1 is the point-in-time distribution and Q2 is maximum.

We define a dictionary with the relevant loadcase names and corresponding variable names form the LSF.

loadcombinations = {'Q1Q2_max':['Q1', 'Q2'], 'Q1_max':['Q1'], 'Q2_max':['Q2']}

Note: The specification of this dictionary is optional. By default, LoadCombination assumes one combination load to act at its maximum in a load case, while the others are considered to be the point-in-time distribution.

Specify user-defined correlation (optional)

The user can also specify a user-defined correlation matrix for the random variables of the reliability problem as a DataFrame.

label_rvs = ["Q1", "Q2", "R", "G"]
corr = np.eye(len(label_rvs))
df_corr = pd.DataFrame(data=corr, columns=label_rvs, index=label_rvs)
corr_Q1Q2 = 0.8
df_corr.loc["Q1", "Q2"] = corr_Q1Q2
df_corr.loc["Q2", "Q1"] = corr_Q1Q2
print(df_corr)

     Q1   Q2    R    G
Q1  1.0  0.8  0.0  0.0
Q2  0.8  1.0  0.0  0.0
R   0.0  0.0  1.0  0.0
G   0.0  0.0  0.0  1.0

Specify user-defined analysis options (optional)

The user can also specify a user-defined correlation Pystra AnalysisOptions object for the reliability analysis too. In this tutorial we will set error thresholds and change the default transform method to use singular value decomposition.

options = ra.AnalysisOptions()
options.setE1(1e-3)
options.setE2(1e-3)
options.setTransform("svd")

Instantiate LoadCombination object

LoadCombination class requires specification of combination distributions as a dictionary, while the other distributions (permanent loads and resistances) are specified as a list.

lc = ra.LoadCombination(lsf=lsf, dict_dist_comb=Q_dict, list_dist_resist=[Rdist], list_dist_other=[Gdist],
                        corr=df_corr, list_const=[cg], opt=options, dict_comb_cases=loadcombinations)

Analyse Load Cases

Use a list to keep track of each Form object outputted:

form = 3*[None]

Load Case 1

lc_idx = 0
form[lc_idx] = lc.run_reliability_case(lcn='Q1Q2_max')
form[lc_idx].showDetailedOutput()

======================================================
FORM
======================================================
Pf                       2.5348733315e-02
BetaHL                   1.9540317148
Model Evaluations        38
------------------------------------------------------
Variable            U_star             X_star        alpha
R                -1.818038           1.898248    -0.930293
G                -0.659741           1.018495    -0.337834
Q1                0.184954           1.423639    +0.095051
Q2               -0.208597           1.759687    -0.106715
cg                     ---           0.400000          ---
======================================================

Load Case 2

lc_idx = 1
form[lc_idx] = lc.run_reliability_case(lcn='Q1_max')
form[lc_idx].showDetailedOutput()

======================================================
FORM
======================================================
Pf                       1.9624337657e-02
BetaHL                   2.0615701821
Model Evaluations        49
------------------------------------------------------
Variable            U_star             X_star        alpha
R                -1.926554           1.896315    -0.934503
G                -0.673345           1.018964    -0.326631
Q1                0.189636           1.461699    +0.091993
Q2               -0.221604           1.596853    -0.107490
cg                     ---           0.400000          ---
======================================================

Load Case 3

lc_idx = 2
form[lc_idx] = lc.run_reliability_case(lcn='Q2_max')
form[lc_idx].showDetailedOutput()

======================================================
FORM
======================================================
Pf                       1.5511691106e-02
BetaHL                   2.1567726618
Model Evaluations        49
------------------------------------------------------
Variable            U_star             X_star        alpha
R                -2.022994           1.894827    -0.937968
G                -0.683828           1.019274    -0.317075
Q1                0.192740           1.386755    +0.089372
Q2               -0.233228           1.888565    -0.108134
cg                     ---           0.400000          ---
======================================================

Display reliability per load combination

for lc,β in zip([k for k in loadcombinations.keys()], [f.beta for f in form]):
    print(f"{lc}: β = {β[0]:.2f}")

Q1Q2_max: β = 1.95
Q1_max: β = 2.06
Q2_max: β = 2.16

Distributions for Load Combinations

Pystra includes a range of tools to enable the calculation of load combinations due to variable loads:

• Zero-Inflated Distributions allow for a probability of non-occurence of a load

• Maximum Distributions allow the distribution of maxima of a supplied parent or point-in-time distribution

• MaxParent Distribution allows the determination of the point-in-time distribution from a supplied maximum.

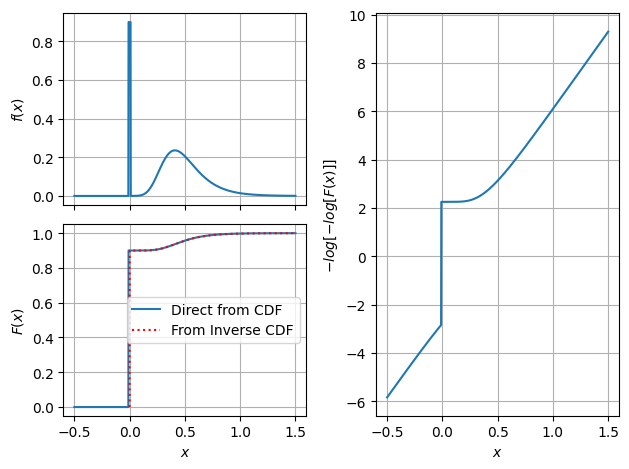
Zero-Inflated Distribution

zin = ra.ZeroInflated('Q',ra.Gumbel("G", 0.5, 0.2),p=0.9)
zin.zero_tol = 1e-2
x = np.linspace(-0.5,1.5,1000)
pdf = zin.pdf(x)
cdf = zin.cdf(x)
u = np.linspace(0,1,10001)
ppf = zin.ppf(u)
fig,axs = plt.subplot_mosaic([['a','c'],['b','c']],sharex=True)
ax = axs['a']
ax.plot(x,pdf)
ax.set_ylabel('$f(x)$')
ax.grid()
ax = axs['b']
ax.plot(x,cdf,label='Direct from CDF')
ax.plot(ppf,u,'r:',label='From Inverse CDF')
ax.set_ylabel('$F(x)$')
ax.set_xlabel('$x$')
ax.legend(loc='center right')
ax.grid()
ax = axs['c']
ax.plot(x,-np.log(-np.log(cdf)))
ax.set_ylabel('$-log[-log[F(x)]]$')
ax.set_xlabel('$x$')
ax.grid()
plt.tight_layout();
#fig.set_layout('tight');

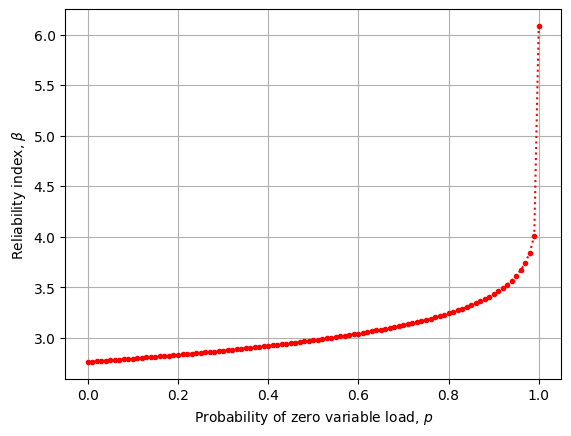
Example

def lsf(R,G,Q):
    return R - (G + Q)

def reliability(p=0.0):
    ls = ra.LimitState(lsf)
    sm = ra.StochasticModel()
    sm.addVariable(ra.Lognormal("R", 6.0,0.15))
    sm.addVariable(ra.Normal("G", 4.5, 0.2))

    g = ra.Gumbel("Q", 0.5, 0.2)
    if p == 1.0:
        sm.addVariable(ra.Constant("Q",0.0))
    elif p == 0.0:
        sm.addVariable(g)
    else:
        zig = ra.ZeroInflated("Q",g,p=p)
        sm.addVariable(zig)

    form = ra.Form(sm,ls)
    form.run()

    return form

betas = []
ps = np.linspace(0,1.0,101)
for p in ps:
    form = reliability(p=p)
    betas.append(form.beta)

fig,ax = plt.subplots()
ax.plot(ps,betas,'r.:')
ax.set_xlabel('Probability of zero variable load, $p$')
ax.set_ylabel('Reliability index, $β$')
ax.grid();