Load Combination Distributions#
Pystra includes a range of tools to enable the calculation of load combinations due to variable loads:
Zero-Inflated Distributions allow for a probability of non-occurence of a load
Maximum Distributions allow the distribution of maxima of a supplied parent or point-in-time distribution
MaxParent Distribution allows the determination of the point-in-time distribution from a supplied maximum.
[1]:
import pystra as ra
import numpy as np
from matplotlib import pyplot as plt
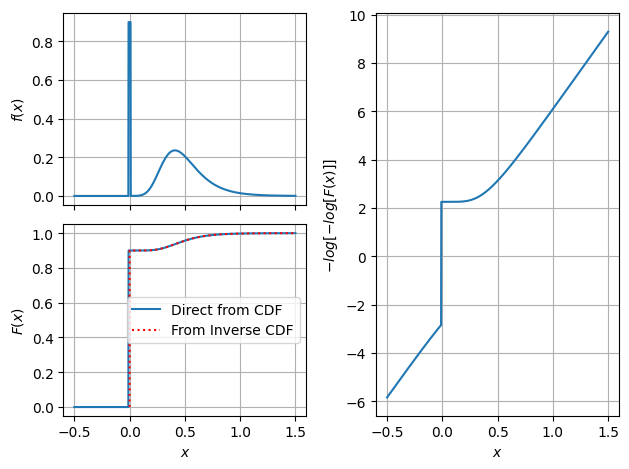
Zero-Inflated Distribution#
[62]:
zin = ra.ZeroInflated('Q',ra.Gumbel("G", 0.5, 0.2),p=0.9)
zin.zero_tol = 1e-2
x = np.linspace(-0.5,1.5,1000)
pdf = zin.pdf(x)
cdf = zin.cdf(x)
u = np.linspace(0,1,10001)
ppf = zin.ppf(u)
fig,axs = plt.subplot_mosaic([['a','c'],['b','c']],sharex=True)
ax = axs['a']
ax.plot(x,pdf)
ax.set_ylabel('$f(x)$')
ax.grid()
ax = axs['b']
ax.plot(x,cdf,label='Direct from CDF')
ax.plot(ppf,u,'r:',label='From Inverse CDF')
ax.set_ylabel('$F(x)$')
ax.set_xlabel('$x$')
ax.legend(loc='center right')
ax.grid()
ax = axs['c']
ax.plot(x,-np.log(-np.log(cdf)))
ax.set_ylabel('$-log[-log[F(x)]]$')
ax.set_xlabel('$x$')
ax.grid()
plt.tight_layout();
#fig.set_layout('tight');
[5]:
def lsf(R,G,Q):
return R - (G + Q)
[63]:
def reliability(p=0.0):
ls = ra.LimitState(lsf)
sm = ra.StochasticModel()
sm.addVariable(ra.Lognormal("R", 6.0,0.15))
sm.addVariable(ra.Normal("G", 4.5, 0.2))
g = ra.Gumbel("Q", 0.5, 0.2)
if p == 1.0:
sm.addVariable(ra.Constant("Q",0.0))
elif p == 0.0:
sm.addVariable(g)
else:
zig = ra.ZeroInflated("Q",g,p=p)
sm.addVariable(zig)
form = ra.Form(sm,ls)
form.run()
return form
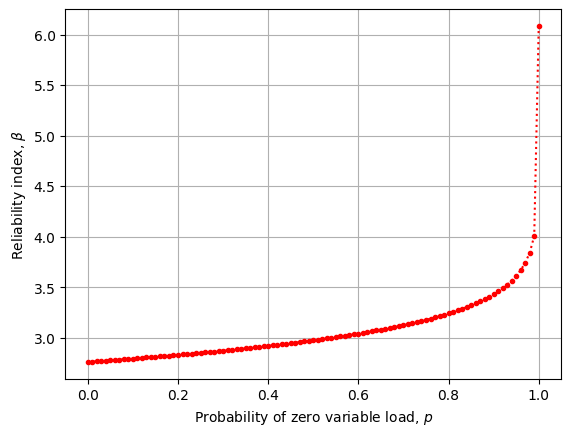
[67]:
betas = []
ps = np.linspace(0,1.0,101)
for p in ps:
form = reliability(p=p)
betas.append(form.beta)
[71]:
fig,ax = plt.subplots()
ax.plot(ps,betas,'r.:')
ax.set_xlabel('Probability of zero variable load, $p$')
ax.set_ylabel('Reliability index, $β$')
ax.grid();
[ ]: